はじめに
 幽灯子/基本情報技術者副専門官
幽灯子/基本情報技術者副専門官私たちが日常で何気なく使っている「小数」。実は小数には 3つの種類 があることをご存じですか?
この記事では「有限小数」「無限小数」「循環小数」について、数学が苦手な方でもスッキリわかるようにやさしく解説します。
そもそも「小数」って何?



小数とは、整数では表しきれない「端数(はすう)」を表すための数の書き方です。
たとえば、ピザを4等分して1切れ食べたとき、食べた量は「0.25枚」。これが小数です。小数点(.)の右側に数字が並び、1より小さい部分を表現してくれます。
この小数点より右に並ぶ数字が どこまで続くか によって、小数は3つの種類に分かれます。
1. 有限小数 ― 終わりがある小数





有限小数とは、小数点以下の数字が 途中で終わる 小数のことです。
具体例
| 分数 | 小数 |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/8 | 0.375 |
| 7/20 | 0.35 |
どれも小数点以下が有限の桁数で「ピタッ」と終わっていますよね。これが有限小数です。
どんなときに有限小数になる?
分数を小数に直したとき、有限小数になるかどうかは 分母 で決まります。分母を素因数分解したとき、2と5だけ で構成されていれば有限小数になります。
たとえば 1/8 の分母「8」は 2×2×2 なので、2だけでできています。だから 1/8 = 0.125 と、きれいに終わるわけです。
一方、1/20 の分母「20」は 2×2×5 なので、やはり2と5だけ。1/20 = 0.05 で有限小数です。
覚え方: 分母が「2と5の仲間」だけなら、小数はきれいに終わる!
2. 無限小数 ― 終わりがない小数



無限小数とは、小数点以下の数字が 永遠に続く 小数のことです。どこまで書いても終わりが来ません。
具体例
- 1/3 = 0.33333…(3がずっと続く)
- π(円周率)= 3.14159265358979…(規則なく続く)
- √2 = 1.41421356…(規則なく続く)
「えっ、1/3 と π って同じ仲間なの?」と思った方、鋭いです。実は無限小数には さらに2つのタイプ があります。
| タイプ | 特徴 | 例 |
|---|---|---|
| 循環小数 | 同じパターンが繰り返される | 1/3 = 0.333… |
| 非循環小数 | パターンがなく永遠に続く | π = 3.14159… |
つまり、無限小数は大きなグループで、その中に「循環するもの」と「循環しないもの」が含まれているのです。
3. 循環小数 ― 同じパターンを繰り返す無限小数





循環小数とは、無限小数の中でも 同じ数字の並びが延々と繰り返される タイプのものです。
具体例
| 分数 | 小数 | 繰り返し部分 |
|---|---|---|
| 1/3 | 0.333… | 3 |
| 1/6 | 0.1666… | 6 |
| 1/7 | 0.142857142857… | 142857 |
| 1/11 | 0.090909… | 09 |
循環小数の書き方
数学では、繰り返す部分の最初と最後の数字の上に 点(ドット) を打って表します。
- 0.333… → 0.3̇(3の上にドット)
- 0.142857142857… → 0.1̇4285̇7̇(1と7の上にドット)
これは「ここからここまでが永遠にリピートしますよ」という印です。
循環小数は分数に戻せる
循環小数の面白いところは、必ず分数で表せるという点です。実際にやってみましょう。
例:0.333… を分数に直す
- x = 0.333… とおく
- 両辺を10倍する → 10x = 3.333…
- 引き算する → 10x − x = 3.333… − 0.333…
- 9x = 3
- x = 3/9 = 1/3
ちゃんと元の分数に戻りましたね。
例:0.090909… を分数に直す
- x = 0.090909… とおく
- 両辺を100倍する → 100x = 9.0909…
- 引き算する → 100x − x = 9.0909… − 0.0909…
- 99x = 9
- x = 9/99 = 1/11
このように、循環小数はちょっとした計算で必ず分数に変換できます。
3つの小数を一目で比較


| 有限小数 | 循環小数 | 非循環無限小数 | |
|---|---|---|---|
| 小数点以下 | 途中で終わる | 永遠に続く(パターンあり) | 永遠に続く(パターンなし) |
| 分数で表せる? | はい | はい | いいえ |
| 数の種類 | 有理数 | 有理数 | 無理数 |
| 身近な例 | 0.5, 0.25 | 0.333…, 0.1666… | π, √2 |
ここで重要なポイントがあります。有限小数と循環小数は、どちらも「分数で表せる数」=有理数です。一方、πや√2のように循環しない無限小数は「分数では絶対に表せない数」=無理数と呼ばれます。
日常生活のどこに関係しているの?



「こんな知識、普段使わないでしょ?」と思うかもしれません。でも、実は意外なところで関わっています。
お金の計算 ― 消費税の計算で「割り切れない」ことがありますよね。たとえば税込み価格を3人で割り勘すると、1/3 = 0.333… となり、1円単位でぴったり割れないことがあります。これはまさに循環小数が原因です。
コンピュータの計算 ― コンピュータは小数を2進数で扱うため、私たちにとって有限小数の 0.1 が、コンピュータの中では無限小数になることがあります。表計算ソフトで合計がわずかにズレる現象は、この仕組みが関係しています。
建築・ものづくり ― 円周率 π は非循環無限小数ですが、円い部品を作るときには必ず登場します。実用上は 3.14 や 3.14159 などに丸めて使います。
まとめ
小数には「終わるもの」と「終わらないもの」があり、終わらない小数にも「パターンがあるもの」と「ないもの」があります。
- 有限小数 → 小数点以下が途中で終わる(例:0.25)
- 循環小数 → 同じ数字のパターンが永遠にリピート(例:0.333…)
- 非循環無限小数 → パターンなく永遠に続く(例:π)
分数で表せるかどうかが「有理数」と「無理数」の境目になっていて、有限小数と循環小数は有理数、非循環無限小数は無理数に分類されます。



普段なにげなく見ている小数の裏側には、こんなに奥深い世界が広がっていたのです。
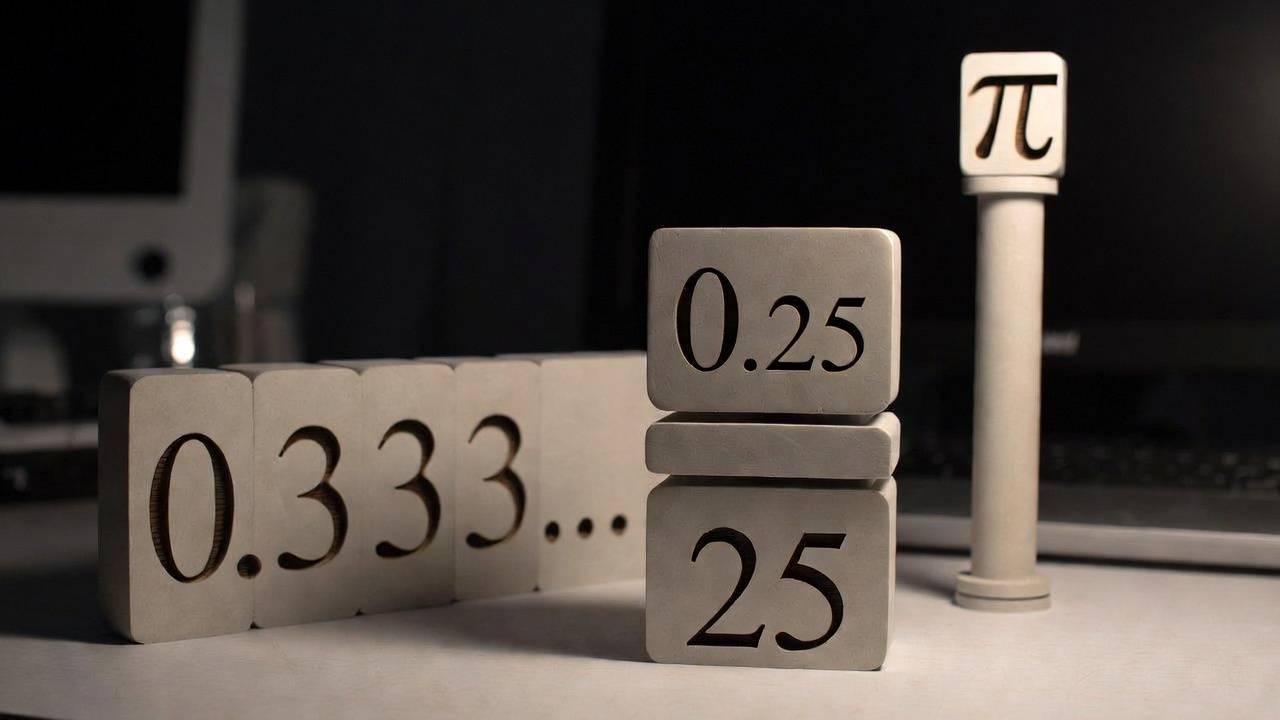









コメント